Recursion is the process by which a function calls itself within the function definition. In this article, I will discuss how to implement recursion and its applications. Recursion is an easy way to solve certain problems, such as tree traversals and the tower of Hanoi. A recursive function solves a specific problem by calling a copy of itself and solving smaller subproblems of the original problems. Recursion is an amazing method that allows us to shorten our code and make it easier to read and write.

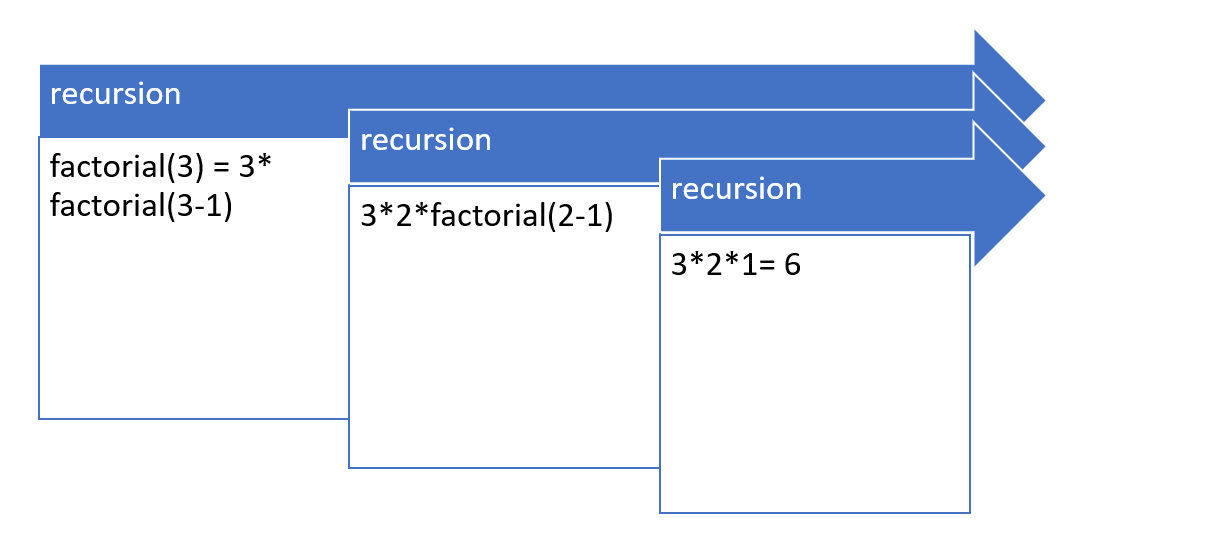
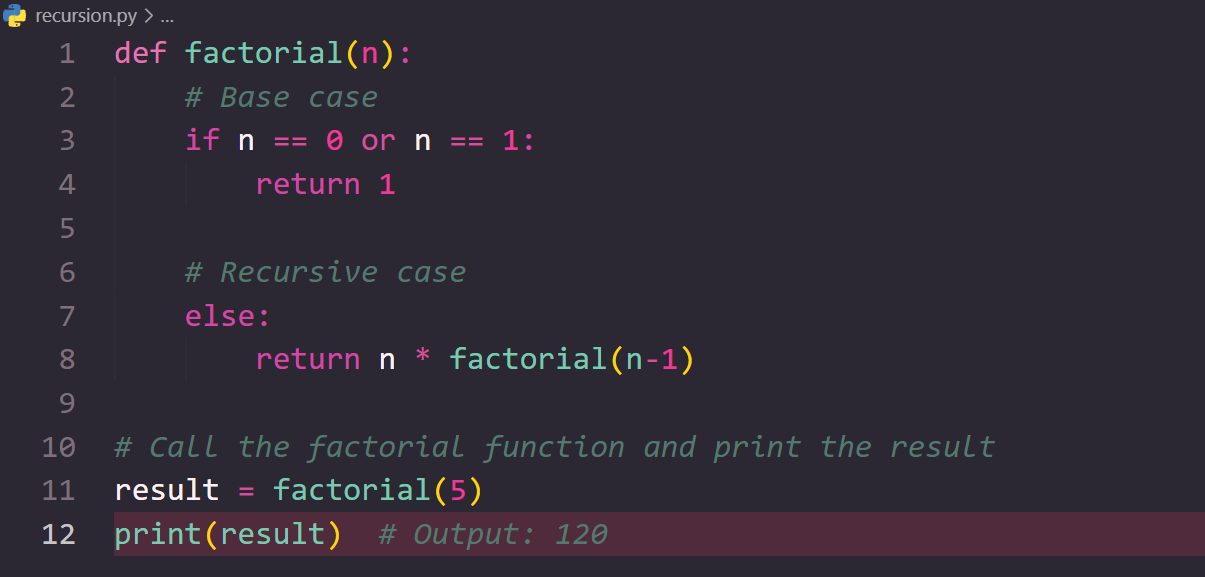
A recursive algorithm can be implemented in a few simple steps. Defining the base case is the first step. This is the most simple scenario for which there is a known or easily accessible solution. This is our stopping point. Defining the recursive case is the next step. This is the process of defining the issue in terms of more manageable subproblems. Divide the problem into smaller subproblems, then call the function repeatedly to solve each one. Thirdly, make sure the recursion doesn't go into an infinite loop and ends when it reaches the base case. The solutions are combined in the final step. Let's solve a problem to learn how to implement a recursive algorithm. The code will compute the factorial for a given number. Let n be the number. The base case is when n is either 1 or 0. In this instance, the response is 1. The process of multiplying n by n-1 is the recursive case. I used Python to implement the code.

A few common applications for recursion include:

Tree and graph traversal: Data structures like trees and graphs are commonly traversed and searched using recursion. A tree or graph can be methodically explored by using recursive algorithms to look at each node or vertex in detail.

Algorithms for sorting: Recursive algorithms are also utilized in merge sort and quicksort. Recursion is used by these algorithms to split the data into smaller sublists or subarrays, sort them, and then combine them back.

Divide-and-conquer algorithms: Recursion is a common technique used by many algorithms that employ a divide-and-conquer strategy, like the binary search algorithm, to divide the problem into smaller subproblems.

Fractal generation: Recursive algorithms can be used to create fractal patterns and shapes. For example, the Mandelbrot set is created by repeatedly applying a recursive formula on complex numbers.

Algorithms for backtracking: These algorithms are employed to address situations in which a series of decisions must be made, each of which is dependent upon the decisions made before it. Recursion can be used to construct these algorithms in a way that explores every path and goes back when a solution cannot be found.

This concludes the article. The completed source code can be found on my GitHub page.